Salut cher(e) ami(e) 👋,
Je sais ! Ça fait deux semaines que tu n'as pas eu de mes nouvelles 😓
Les journées se sont enchaînées à un rythme fou, la maladie est passée par là, les copies se sont entassées et le temps a beaucoup manqué. Mais je suis de retour et j'espère que tu es prêt pour un nouveau numéro de la lettre du dimanche !
Sur les dernières semaines, j'ai fait passer les premières évaluations en mathématiques et j'en ai corrigé pas mal. Les résultats sont un peu mitigés, mais je suis confiant pour la suite. Suite à cela, j'ai eu une discussion assez intéressante avec certains de mes élèves sur la bonne approche des mathématiques au lycée. Je sais que j'en ai déjà parlé à plusieurs reprises ici, mais puisqu'il y a des nouveaux permet moi de t'en parler une dernière fois (et oui ! La Newsletter du dimanche a de plus en plus de succès 😊).
Allez sans trop tarder ! Voici le programme d'aujourd'hui :
🎯Quality over quantity ! La recette gagnante.
À quoi servent ces mathématiques ? Je ne compte plus le nombre de fois qu'on m'a posé cette question en dix ans de carrière. En général, j'ai souvent tendance à répondre : d'un point de vue pratique...peut-être à rien !
Ma réponse un peu provocatrice fait toujours son effet. Bien évidemment que les mathématiques servent à quelque chose. Sauf que les élèves posent souvent cette question dans l'optique d'avoir, en réponse, une application pratique...Une finalité.
Je ne suis pas d'accord avec cette façon de voir les choses. Dans beaucoup d'aspects de la vie, le voyage est plus important que la destination. Ce qu'apportent réellement les mathématiques avant tout, c'est une façon de réfléchir et de raisonner. Il y a certes le savoir disciplinaire également, mais c'est surtout la méthodologie de réflexion rigoureuse que tous les élèves emmènent, avec eux, dans la vie de tous les jours.
En partant de ce constat, avoir une approche quantitative et mécanique lorsque tu fais tes exercices de mathématiques n'a aucun sens. Si l'objectif est de comprendre en profondeur la nature des situations et des notions, il vaut alors mieux faire très peu d'exercices très qualitatifs et qui poussent à la réflexion. Passer du temps sur les démonstrations du cours et sur la compréhension des objets mathématiques que tu manipules est également très primordial.
Donc si tu veux réellement améliorer ton niveau en mathématiques au lycée, je te conseille sérieusement d'abandonner la méthodologie qui consiste à faire des tonnes d'exercices sans aucun objectif précis. Garde toujours ceci en tête :
Quality over quantity !
🪄 15...comme la constante du carré magique d'ordre 3
Le nombre de la semaine est le 15. Celui-là, je l'attendais avec impatience !
Il y a énormément de choses à dire à son propos. C'est par exemple un nombre semi-premier, un nombre de Bell, un nombre triangulaire, la somme des trois premiers nombres impairs (3;5;7) et ainsi de suite.
Mais s'il y a un sujet qui me fascine tout particulièrement à propos de ce nombre, c'est qu'il est la constante du plus célèbres des carrés magiques.
Ah ? Tu veux savoir ce que c'est qu'un carré magique ? Eh bien c'est un tableau avec autant de lignes et de colonnes que tu remplis avec des nombres. Un peu comme un Sudoku. À un détail près...Il y a une règle pour différente pour le remplir.
Il faut que la somme des nombres sur chaque ligne, chaque colonne et chaque diagonale soit égale au même nombre. On appelle ce dernier la constante magique.
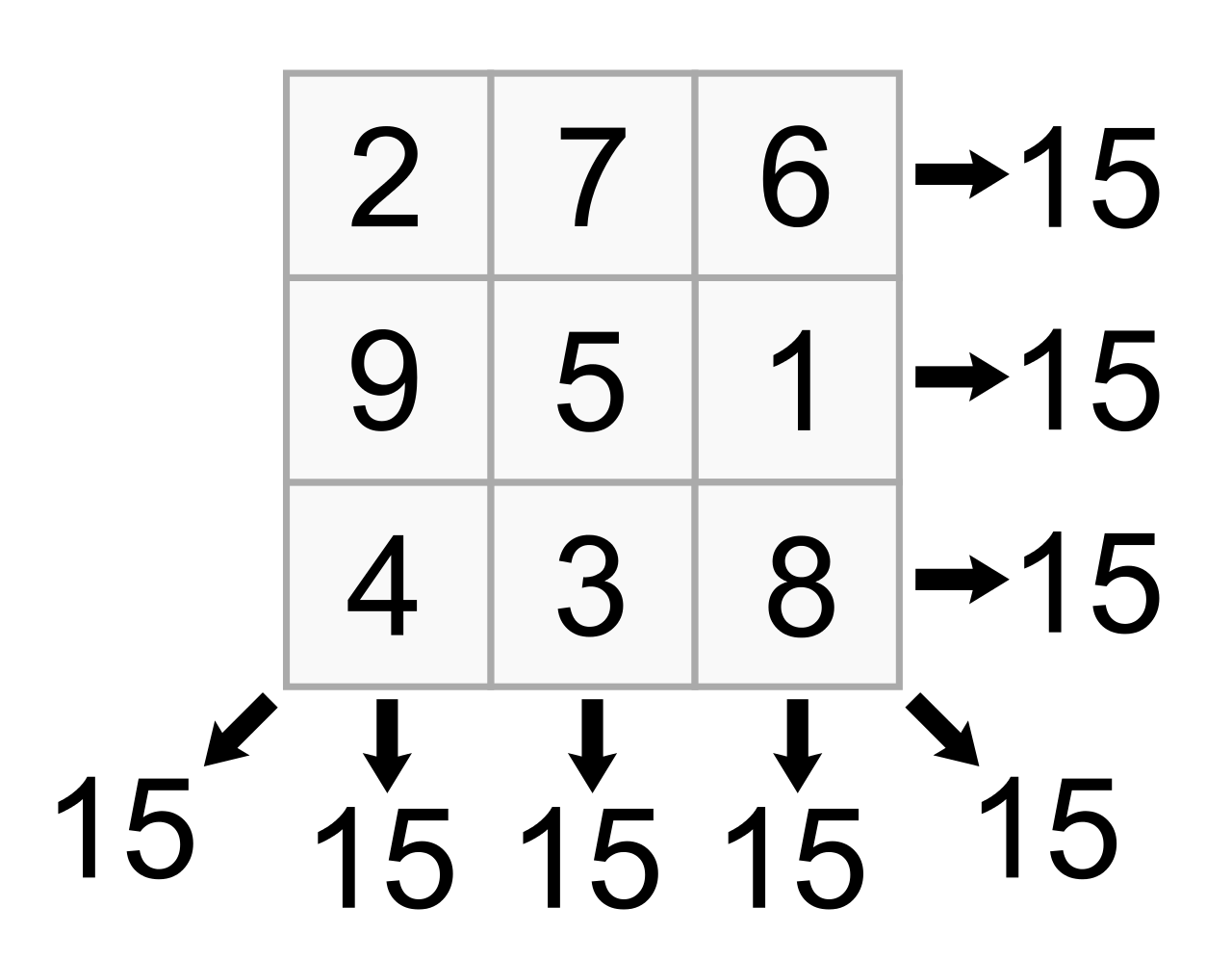
J'ai personnellement passé beaucoup de temps à étudier les propriétés de ces carrés. Plus on augmente l'ordre, plus ils deviennent intéressants.
W.Rouse Ball leur consacre un chapitre entier dans le troisième tome de son livre : Récréations mathématiques. Tu peux également trouver des traces de ces carrés dans plusieurs œuvres artistiques. Voici quelques exemples : (Je te laisse trouver le carré magique de chacun des exemples. Ps : Ce n'est pas 15 😉)
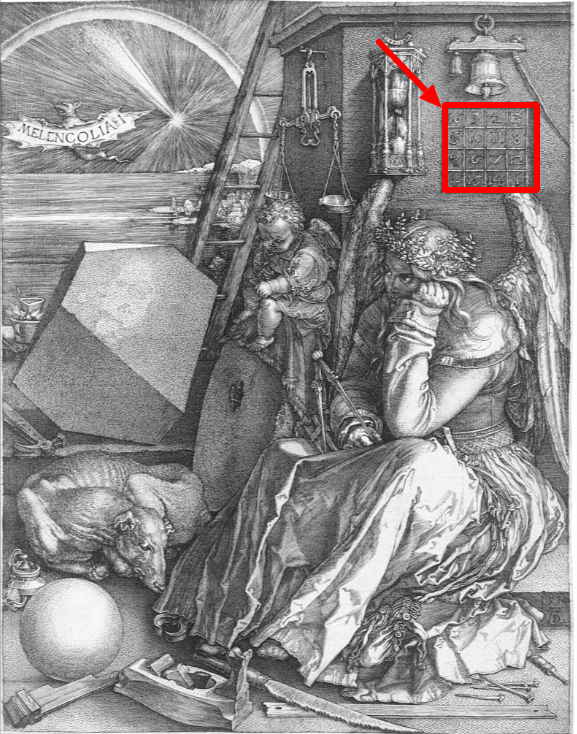

🎨Les mathématiques dans l'art.
Puisqu'on parle des arts, allons un peu plus loin pour voir à quel point les mathématiques sont présentes...là où on s'y attend le moins !
La divine proportion : un classique.
Connu aussi sous le nom du nombre d'or. C'est de loin le nombre mathématique le plus représenté en art. Il représente la perfection proportionnelle.
\[ \Phi=\dfrac{1+\sqrt{5}}{2}\]
Les peintres, les sculpteurs et les architectes l'utilisent excessivement. Le motif géométrique qui le représente le plus est la spirale. On peut par exemple le retrouver dans la vague de Hokusai :

Ou encore dans le logo d'Apple :

Tu peux également le retrouver dans la Joconde, l'homme de Vitruve, la cène...
L'infini : l'art des paradoxes
L'infini est l'un des concepts mathématiques les plus fascinants. Il n'est donc pas surprenant que les artistes s'en emparent rapidement. C'est par exemple le cas d'Escher, l'un de mes artistes favoris.
Ce génie adore jouer avec les paradoxes des boucles infinis. Je te laisse admirer certaines de ses œuvres pour t'en rendre compte :
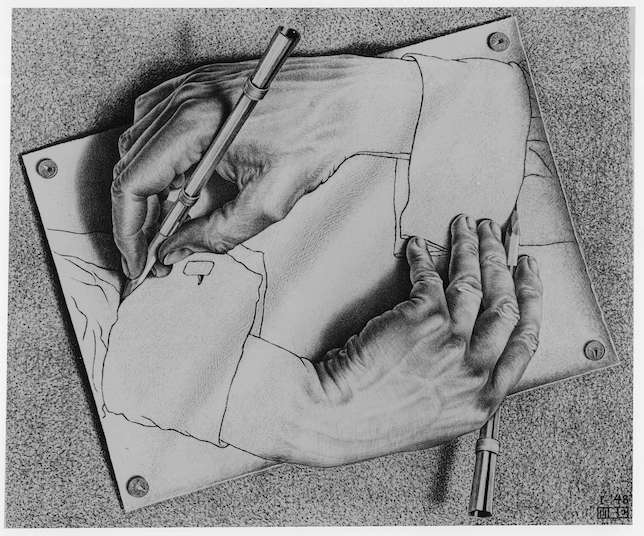



📖 Lecture de la semaine : Gödel, Escher, Bach, Les Brins d'une Guirlande Éternelle.
Si la discussion que nous venons d'avoir t'a intéressé, alors le livre de cette semaine est un must read pour toi ! Il s'agit de Gödel, Escher, Bach, Les Brins d'une Guirlande Éternelle de Douglas Hofstadter.
C'est un vieux livre qui a été écrit en 1979. Un classique de genre qui fait le lien entre mathématiques, arts et musique. Il contient également des réflexions sur l'intelligence artificielle. Chose très surprenante vu sa date de sortie.

🎦 Youtube Math find : Alain Aspect est lauréat du Nobel de Physique 2022.
Bon, je ne pouvais pas t'écrire cette semaine sans mentionner cet événement majeur ! Alain Aspect vient d'être nommé Nobel de Physique de l'année.
Ce qui m'a le plus touché personnellement, c'est que dans son discours, la première personne qu'il cite est son professeur de physique de terminale ! Cela montre vraiment à quel point mon métier a du sens...Même si les conditions de travail et la considération de la société ne sont pas toujours au rendez-vous, c'est ce type d'événement qui me pousse à continuer dans ma mission !
Je te laisse visionner son petit discours 👇
💞 Mes coups de cœur de la semaine
Un article sur une avancée autour de la conjecture de Sullivan : J'ai découvert cette conjecture lors de mes études universitaires à la Sorbonne. Depuis, je maintiens toujours une petite vieille autour de ce thème et il se trouve qu'il y a du nouveau ! L’article suivant (en anglais) explique en détail le sujet 👇
Une rencontre avec certains de mes anciens élèves : Comme tu le sais déjà, j'adore rencontrer mes anciens élèves. C'est de loin, la partie la plus agréable de mon métier. Donc merci à Emma, Angélina, Julien et Margaux pour le café d'hier. C'était un réel plaisir de vous revoir et d'avoir de vos nouvelles !










Discussion entre membres