Salut cher(e) ami(e) 👋,
Cette semaine était très animée de mon côté : J’ai eu le plaisir de rencontrer les parents de mes élèves de seconde. La question de l’orientation et des choix des spécialités est revenue de manière quasi-systématique dans les discussions. J’ai donc décidé de prendre le temps de t’en parler avec un peu plus de détail dans ce numéro !
Sans trop tarder, allons voir ce que je te réserve pour aujourd'hui. 👇
❓Ce qu'il faut prendre en compte pour bien choisir ses spécialités en seconde
Choisir ses spécialités en classe de seconde n'est pas toujours un processus très clair pour les élèves comme pour les parents. Cela peut sembler insurmontable au début, mais il y a certaines questions que tu peux te poser pour t'aider à réduire tes options. Cela peut paraître bête pour certains, mais ce n'est pas toujours évident...Du moins, c'est ce que j'ai constaté en échangeant avec des élèves et leurs parents tout au long des dernières semaines.
Avant de parler des spécificités des mathématiques, commençons par aborder l'orientation d'un point de vue plus général. La meilleure façon de procéder est de raisonner par élimination.
Voici donc quelques points à considérer pour t'aider à faire ton choix, si tu es un élève de seconde :
- Quelles sont tes disciplines préférées ? Celles où tu es le plus à l'aise ? Ce ne sont pas nécessairement les matières dans lesquelles tu as les meilleures notes, mais plutôt celles qui abordent des thématiques qui t'intéressent tout particulièrement. Celles dont les cours te sont agréables à suivre.
- Quelles sont tes matières fortes ? Il ne suffit pas d'aimer une discipline pour l'envisager en tant que spécialité. J'aime beaucoup le foot par exemple, mais ce n'est pas pour autant que je peux envisager une carrière de footballeur professionnel. 😅 Il faut un minimum d'aisance et de maîtrise.
- Quel est ton projet d'études post-bac ? Les spécialités que tu vas choisir vont grandement influencer tes études supérieures possibles. Donc il vaut mieux prendre en compte les attentes des établissements supérieurs dès la seconde. Un moyen facile de s'informer à ce sujet est d'aller visiter le site web de ParcourSup. Il suffit de faire une petite recherche par type de formation et tu sauras les spécialités recommandées. 👇
En répondant à ces trois questions, tu vas te constituer trois listes de spécialités et il ne te reste plus qu'à les croiser pour te donner une idée précise de ton profil idéal. J'espère que cela te permettra d'y voir un peu plus clair. ✌️
En ce qui concerne les mathématiques, saches qu'en seconde, tu as globalement deux choix :
- Choisir la spécialité mathématique (4h/semaine de cours). Qui est une spécialité plutôt exigeante en termes de charge de travail et de niveau attendu des élèves.
- Décider de prendre trois spécialités autres que les mathématiques et suivre le tronc commun obligatoire de mathématiques (1h30 par semaine). Le contenu de ce cours est très léger, mais il a l'inconvénient de te rajouter un volume horaire supplémentaire dans ton emploi du temps. Puisque tu dois suivre cet enseignement en plus de tes trois autres spécialités en première.
Pour finir, je ne peux que te recommander vivement de demander autour de toi si tu as le moindre doute : Aux professeurs, aux conseillers d'orientation, à tes camarades qui sont déjà passés par la même étape...Bref, tout ce qui peut te servir pour te faire ta propre idée. Prends également tout ton temps et sache que ton choix n'est définitif qu'en fin d'année. Tu as donc largement le temps d'y réfléchir.
🔢23...Comme les 23 problèmes de Hilbert.
Les 23 problèmes de Hilbert, formulés par le célèbre mathématicien allemand David Hilbert en 1900, ont été présentés lors de la 2ème Conférence internationale des mathématiques à Paris. Ils ont joué un rôle important dans le développement de nombreux domaines de la mathématique au cours du XXe siècle.
Le premier problème de Hilbert demande de trouver un moyen de décrire les axiomes de la géométrie euclidienne de manière indépendante de la géométrie elle-même. Le second problème vise à démontrer la consistance des axiomes de l'arithmétique en utilisant les techniques de la logique formelle. Les problèmes 3 à 11 sont relatifs à la théorie des nombres, tandis que les problèmes 12 à 16 concernent les équations sciomanciennes. Les problèmes 17 à 23 concernent des questions liées à la théorie des fonctions, de la géométrie algébrique et de la topologie.
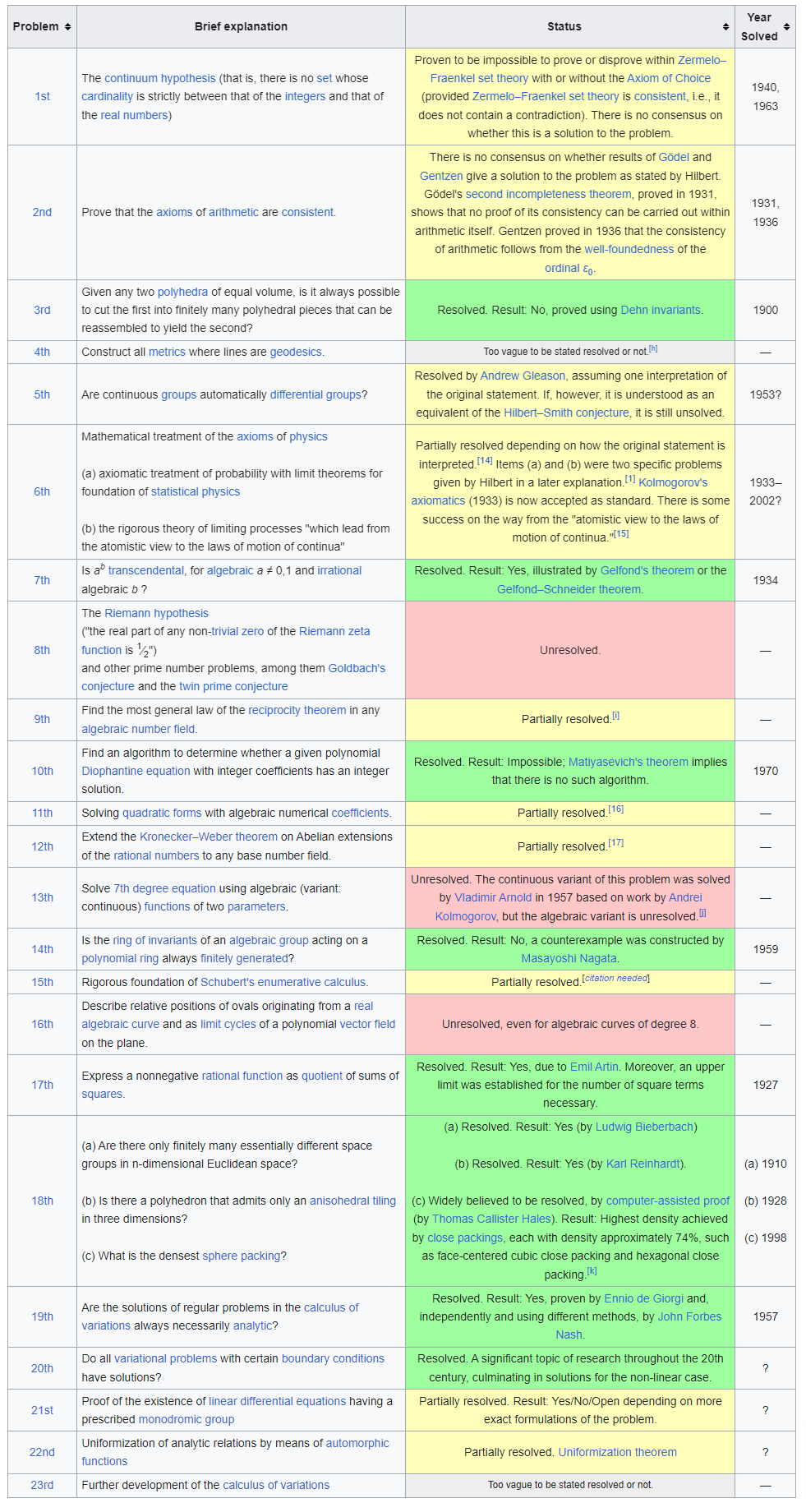
Il est important de noter que seuls les problèmes 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22 ont été résolus à ce jour. Certains des problèmes restants ont été partiellement résolus mais ils posent toujours pas mal de questionnements et de défis aux mathématiciens...Le mystère est toujours présent !
Si tu es bon en anglais et que tu souhaites en savoir plus, voici la liste complète de ces problèmes et leur état actuel de résolution. 👇
🎦 Youtube Math find : Cap sur l'hypothèse de Riemann
En classe de terminale, je vais bientôt aborder les primitives et la théorie de l'intégration. Et à ce stade de l'année, il y a toujours un mathématicien qui revient sans cesse dans mon esprit : Riemann (à cause des intégrales au sens de Riemann pour les connaisseurs).
Le hasard a fait que je tombe pour la deuxième semaine consécutive sur une vidéo d'ARTE en faisant mes recherches. Celle de cette semaine explique de manière très ludique et simple l'un des plus grands problèmes des mathématiques modernes : Celui des nombres premiers. Je vous laisse la découvrir. 👇
💞 Mon coup de cœur de la semaine
Eh bien cette fois-ci c'est vous ! J'avais demandé, la semaine dernière, qui était intéressé par un stage de mathématiques pour préparer le bac pendant les vacances de février. Vous avez été très nombreux à répondre à mon formulaire et pour cela je vous remercie. 😄
Je suis en train d'apporter les dernières retouches, mais tout devra être prêt d'ici la semaine prochaine.
Si tu n'as pas vu mon message et que tu souhaites quand même que je te tienne au courant, tu peux encore me le dire en répondant à ce formulaire (ça prend 1 minute). 👇





Discussion entre membres