Salut cher(e) ami(e) 👋,

J’espère que tu as passé une bonne semaine ? De mon côté, elle a été un peu dense : conseils de classe, deadlines pour corriger, écrire des appréciations… Bref, la totale comme à chaque fin de trimestre.

Si tu es en terminale, la semaine prochaine est décisive pour toi ! Il est temps de finaliser tes révisions, faire les derniers approfondissements et te préparer mentalement à affronter les épreuves de spécialité qui auront lieu le 20 et 21 Mars.

J’espère que tu es prêt ? Tu trouveras mes derniers conseils concernant cette échéance ci-dessous 👇

Mais avant cela, commençons par l’intro habituelle 😉

📲
Si tu aimes ce que je te propose ici, je t'invite à nous suivre également sur Instagram.

✒️5 derniers conseils pour préparer ton épreuve.

Bon à ce stade de l’année, et vu l’élève sérieux que tu es 😉, je pars du principe que tu es déjà bien avancé dans tes révisions. Voici donc mes derniers conseils pour finir tes préparatifs en beauté :

  1. Fait des fiches avec toutes les formules !
    Un oubli peut toucher n’importe qui, surtout avant les épreuves avec le stress qui monte ! Un bon moyen de ne rien oublier est la traditionnelle fiche de formules qui a fait ses preuves. Tu pourras la consulter une dernière fois juste avant l’examen. La construire te permet également de faire un dernier tour de toutes les notions.
  2. À ce stade, ne fait plus que des annales du bac.
  3. N’oublie surtout pas de t’entraîner à tenir le temps de l’épreuve !
    En te chronométrant notamment. Répondre correctement, c’est bien… Finir l’épreuve dans les temps en plus c’est mieux 😉
  4. Si tu as un doute… Demande à un expert.
    Vu le temps restant, tu n’as plus le luxe d’essayer de comprendre par toi-même des notions : Cela te fera perdre un temps fou ! Alors si tu as un doute ou une incompréhension, demande à un de tes camarades de t’expliquer ou encore mieux : à ton professeur. P.s : Tu peux également m’écrire via e-mail si nécessaire. 😀
  5. Repose-toi suffisamment la veille des épreuves.
    Évite de veiller tard pour réviser le jour avant l’épreuve. Tu as intérêt à être en forme physiquement pour tenir les deux épreuves de 4 heures.

Voilà ! J’espère que cela t’aidera à envisager la suite sereinement. N’hésite surtout pas à me demander de l’aide en cas de besoin. ✌️

🥧Sujet Grand Oral : Les différentes façons d'approximer π !

Dans deux jours, c'est la Journée de π ! Chaque année, le 14 mars (ou le 3/14 en format américain), le nombre mathématique π est célébré. Je pense que je ne t’apprends rien en te rappelant que cette constante mathématique fascinante représente la relation entre la circonférence et le diamètre d'un cercle.

Vu la date assez spéciale, je me suis dit qu’il serait intéressant de te proposer un sujet de grand oral autour de cette thématique. Tu peux t’intéresser par exemple à la problématique suivante :

Approximer π, évolution de la méthode dans l’histoire des mathématiques.

Depuis l'Antiquité, les mathématiciens ont tenté d'approximer π avec de plus en plus de précision. Voici une liste non exhaustive de ce que tu peux explorer et présenter en grand oral :

1. Une méthode de l'Egypte ancienne (2650 avant J.C. - 2100 avant J.C.)

Les anciens Égyptiens ont approximé π en utilisant la méthode de l'aire d'un octogone régulier inscrit dans un cercle. Ils ont constaté que la longueur du côté de l'octogone était égale au rayon du cercle, et que l'aire de l'octogone était égale à l'aire du cercle. En utilisant cette méthode, ils ont approximé π à environ 3,16.

2. Une méthode de l'Inde ancienne (vers 800 avant J.C.)

Les mathématiciens indiens ont approximé π en utilisant la méthode de l'aire d'un carré inscrit dans un cercle. Ils ont constaté que la diagonale du carré était égale à deux fois le rayon du cercle. En utilisant cette méthode, ils ont approximé π à environ 3,125.

3. Une méthode de l'Antiquité grecque (vers 250 avant J.C.)

Le mathématicien grec Archimède a utilisé une méthode géométrique pour approximer π. Il a inscrit et circonscrit des polygones réguliers à un cercle, en utilisant des polygones de plus en plus grands pour se rapprocher de la circonférence du cercle. En utilisant cette méthode, Archimède a approximé π à environ 3,141.

4. Une méthode de la Renaissance (vers 1590)

Le mathématicien français François Viète a utilisé la méthode des fractions continues pour approximer π. Il a défini une série infinie de fractions continues qui convergeaient vers π. En utilisant cette méthode, Viète a approximé π à environ 3,1415926535.

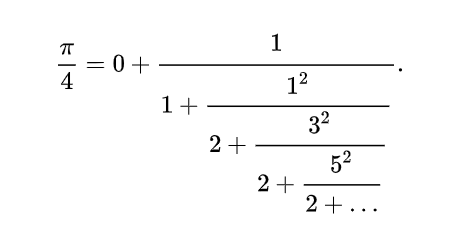
Une approximation possible de π avec des fractions continues

5. Une méthode moderne (à partir du XVIIIe siècle)

Depuis le XVIIIe siècle, les mathématiciens ont utilisé des méthodes modernes pour approximer π, telles que les séries de Taylor et les intégrales. Ces méthodes sont basées sur le calcul numérique et l'analyse mathématique. Je peux citer l’intégrale de Wallis comme exemple concret.

🔢29...comme un nombre premier de Sophie Germain.

Le numéro de la semaine est l'occasion de mettre à l'honneur une des grandes dames des mathématiques : Sophie Germain.

Avant de te parler de la mathématicienne, laisse-moi te définir ce que s’est qu’un nombre premier qui porte son nom.

C’est tout simple :

On dit qu’un nombre x est premier de Sophie Germain si 2x+1 est également un nombre premier.

Il se trouve que le nombre 29 vérifie cette propriété (59=2x29+1 est également premier).

Sophie Germain.

Revenons maintenant à la mathématicienne : Sophie Germain est une mathématicienne française née en 1776. Malgré les obstacles qu'elle a rencontrés en tant que femme dans un monde dominé par les hommes, elle a réussi à faire des contributions importantes à la théorie des nombres et à la physique mathématique.

Elle a commencé à étudier les mathématiques à l'âge de 13 ans, en secret, car ses parents ne voulaient pas qu'elle s’y intéresse. Elle a utilisé le nom d'emprunt "Monsieur Antoine-Auguste Le Blanc" pour correspondre avec deux des plus grands mathématiciens de l'époque : Adrien-Marie Legendre et Carl Friedrich Gauss.

Elle est surtout connue pour sa contribution à la "conjecture de Fermat", qui est l'un des problèmes les plus célèbres de l'histoire des mathématiques (J’en parle en détail ici). Elle a également travaillé sur l'élasticité des corps et a découvert une loi mathématique importante connue sous le nom de "loi de Germain".

Elle a été reconnue pour ses contributions à la mathématique et à la science, et a été la première femme à recevoir une médaille de la Royal Society of Sciences de Bruxelles en 1816. Elle est décédée en 1831 à l'âge de 55 ans.

🎦Youtube Math find : Anecdotes sur l'ENS !

Tous les mathématiciens français connaissent la légende de l’ENS et des brillants “cerveaux” qui ont fait leurs études dans cette grande institution. Voici une petite vidéo qui raconte quelques anecdotes intéressantes à ce sujet. Prépare-toi à voir le monde des mathématiques différemment après cela ! 😅

💞 Mon coup de cœur de la semaine.

Pour cette semaine, le coup de cœur ultime a été la découverte de la chaîne Youtube d'Axel Arno. Si tu as visionné la vidéo ci-dessus, alors tu viens de voir une de ses créations. Si j'ai bien compris, c'est un étudiant en Master de mathématiques qui a pour projet de devenir professeur. Il est passé par la prépa et a une grande culture mathématique doublée d'un grand humour qui m'a déjà poussé à voir plusieurs de ses vidéos. Bref, je recommande ! ✌️