Salut cher(e) ami(e) 👋,
Je vais commencer par remercier tous ceux qui ont répondu à mon petit questionnaire la semaine dernière. C'était vraiment chouette. 😊
Si vous n'avez pas eu le temps de le faire et que vous souhaitez contribuer à l'amélioration de ce que je vous propose ici, vous pouvez toujours faire des suggestions ici. 👇
En plus de l'habituelle rubrique du grand oral et de la vidéo de la semaine, je vais aborder d'un sujet qui me tient à cœur : l'état de l'enseignement de mathématiques au lycée. Surtout depuis la réforme ! L'objectif n'est point de me plaindre gratuitement, mais plutôt de te dire la réalité en face. Si par chance, tu es encore un élève en seconde ou en première...ce que je vais dire pourrait t'être utile.
Mais avant cela, commençons par l’intro habituelle 👇
🏫La réalité des mathématiques au lycée depuis la réforme.
Je vais commencer par faire un petit éclaircissement:
Mon objectif n'est pas de critiquer le système gratuitement, ni de dire que c'était mieux avant ! Je veux juste attirer ton attention sur certains faits et te proposer des solutions. Bien sûr, tout ce qui suivra n'est qu'un avis personnel qui n'engage que moi.
Cette année scolaire marque la première implémentation complète de la réforme du lycée telle qu'elle a été pensée en 2019. Les contraintes sanitaires ayant retardé la mise en application de tous les dispositifs. En particulier, les examens de spécialités qui se déroulent en avril au lieu de juin.
Maintenant que j'ai un aperçu général sur cette réforme je peux commencer à tirer quelques conclusions :
- Le niveau global des mathématiques a baissé : La réforme avait pour but d'augmenter le niveau d'exigences dans les enseignements de spécialité. Et si cette promesse a été tenue dans certaines disciplines (HGGSP par exemple), c'est tout a fait le contraire qui c'est produit en mathématiques à cause du point qui va suivre.
- Des classes plus hétérogènes et un enseignement peu adapté à une grande partie des élèves : Le programme de la spécialité mathématique est ambitieux, c'est une évidence. Mais c'est justement ce point-là qui va causer sa perte.
L'idée de départ, c'est que ce programme soit suivi par des élèves à forte appétence et intérêt pour les mathématiques...des élèves qui ont pour vocation de faire des études hautement scientifiques et qui sont prêts à digérer le grand niveau d'abstraction de la spécialité. Sauf qu'en réalité, cette spécialité est choisie par un très grand nombre d'élèves en raison des conditions d'accès à certaines formations du supérieur. Ces derniers n'ont pas vraiment besoin d'un bagage mathématique élevé et n'éprouvent pas vraiment un intérêt immense pour la discipline...Pour eux, c'est juste un moyen d'accéder à des études de commerce par exemple. Malheureusement...la réforme n'a pas pensé à eux !
Et comme il faut absolument que tout le monde aient le bac, la seule solution du professeur est souvent de diluer le cours, les exercices et même les examens nationaux. - Un examen national décevant : Ce contexte a fait que l'examen de spécialité mathématique est devenu une farce ! Dans un passé pas si lointain, seuls les professeurs se plaignaient de la facilité du sujet...aujourd'hui, même les élèves les trouvent ennuyant et sans aucun intérêt. Comment voulez-vous avoir un bon niveau d'exigence envers des élèves lorsque leur moyenne à l'examen est au-dessus de 17 ? Si l'examen est aussi facile, alors pourquoi s'embêter à travailler dur ?
- Les grands perdants (parce qu'il y en a toujours !) : Ce contexte est extrêmement défavorable aux très bons élèves. Après tout, comment se démarquer quand tout le monde à plus de 17 ? Votre 19/20 au bac perd tout de suite toute sa valeur. En plus de ça, les élèves qui nourrissent des ambitions d'études scientifiques exigeantes se rendent assez vite compte du gouffre qui sépare ce qu'ils ont étudié au lycée avec ce qui est réellement attendu d'eux. Pour vous donner un exemple, voici un lien vers ce qu'attendent les professeurs de Louis Le Grand et Henri 4 d'un élève de terminale qui souhaite intégrer une classe préparatoire. 👇
Cette réalité fait que l'écart entre ceux qui savent ce qui se passe et qui prennent des mesures pour y remédier et entre ceux qui ne le savent pas ne cesse de se creuser. C'est pour cette raison que j'essaye de t'expliquer tout cela aujourd'hui...comme ça, tu sauras ! 😉
🤔Que faire alors ?
Maintenant que nous avons dressé ce tableau un peu sombre, il y a un seul point positif que je peux souligner :
Un élève qui prend au sérieux son apprentissage des mathématiques va se démarquer beaucoup plus facilement dorénavant !
Car il suffit de peu maintenant pour ce hisser au-dessus du lot ! Si tu es un élève en seconde ou en première et que tu as des ambitions mathématiques respectables, je te conseille d'envisager sérieusement l'idée d'apprendre les mathématiques de ton côté et de ne plus attendre tout de ton professeur. Car ce dernier est souvent enchaîné par beaucoup de contraintes en classe. Voici quelques idées :
- Achète des livres plus exigeants que les manuels scolaires et travaille-les sur ton temps libre.
- Si tu as accès aux cours de mathématiques des grands lycées, n'hésite pas à les consulter.
- Demande l'aide de ton professeur en demandant des approfondissements.
Quant à moi, je réfléchis également à des solutions à mettre en place pour mes élèves à partir de l'année prochaine. J'ai plusieurs pistes, mais les contraintes systémiques font que je vais devoir les proposer à titre privé malheureusement. Je vais probablement t'en parler davantage dans un futur proche.
🌍Sujet Grand oral : Volume d'une boule...sans intégrales !
Tout le monde sait que le volume d'une boule de rayon R, se calcule avec la formule :
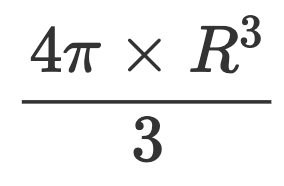
Mais est-ce que tu t'es déjà posé la question de comment démontrer ce résultat ?
Archimède est vraisemblablement le premier à l'avoir fait. Il a publié un traité à ce sujet intitulé : De la sphère et du cylindre (c. 225 av. J.-C.).
La méthode la plus utilisée de nos jours pour prouver cette formule est d'utiliser des intégrales. En ce qui concerne cette idée de grand oral, je te propose plutôt d'utiliser les propriétés des limites des suites. Tu peux donc présenter la problématique suivante : 👇
Comment démontrer le volume d'une boule grâce à la somme des termes d'une suite ?
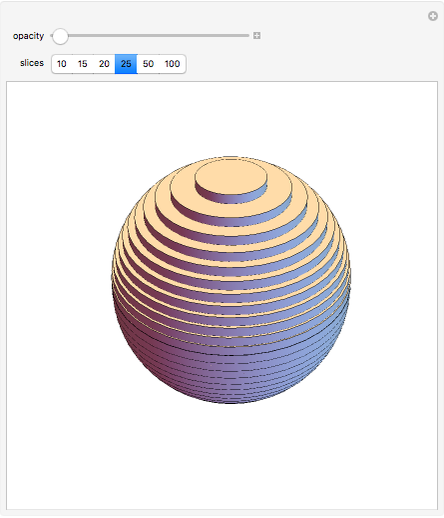
L'idée est assez simple : Il suffit d'empiler des cylindres à l'intérieur d'une sphère comme ceci :
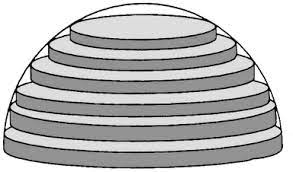
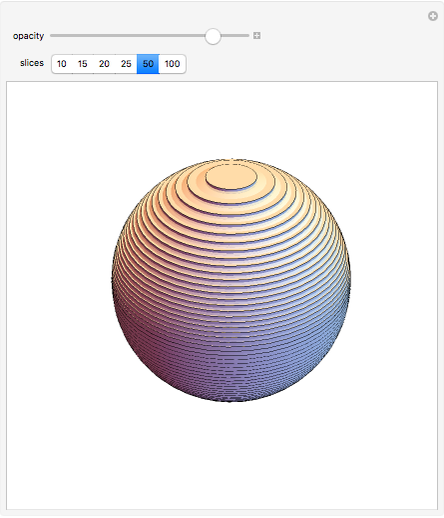
Ainsi, tu peux approximer le volume voulu avec la somme des n premiers termes d'une suite qui décrit les volumes successifs des cylindres empilés. Pour finir, il ne te restera plus qu'à déterminer l'expression du terme général d'une telle suite en fonction du rayon R puis de calculer la limite de la somme lorsque tu fais tendre n vers l'infini afin de gommer les vides entre les cylindres.
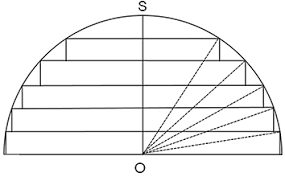
Tu l'auras compris, plus il y a de cylindres, mieux est l'approximation !
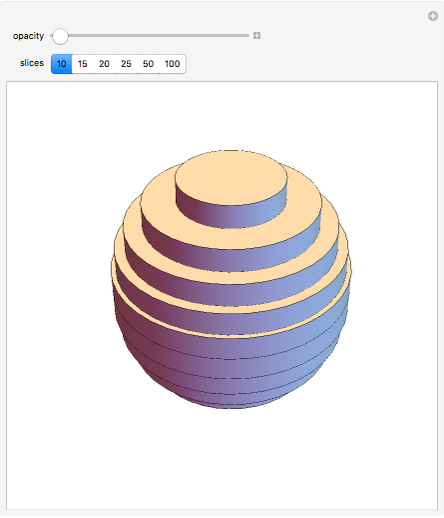
🎦 Youtube Math find : Le paradoxe de Simpson
Comme tu le sais, j'adore les paradoxes ! En voici un qui est lié aux études statistiques. Il peut faire l'objet d'une problématique du grand oral. Je te laisse le découvrir tranquillement 😉
💞 Mon coup de cœur de la semaine
Mon coup de cœur de la semaine n'est rien d'autre que le document que je t'ai suggéré au début de cette lettre. J'ai feuilleté par curiosité les exercices proposés par mes collègues de Louis Le Grand et Henri 4 et j'ai été impressionné par le travail qu'ils ont dû abattre pour proposer une collection aussi riche. Je te conseille vivement sa lecture.










Discussion entre membres