Salut cher(e) ami(e) 👋
Nous sommes bientôt arrivés à la fin de l'année scolaire. Pour les professeurs, c'est souvent synonyme de beaucoup de corrections, de deadlines et d'un sentiment de travail accompli.
Ma semaine a été dense : Je suis allé visiter le salon Lerning Technologies en quête d'inspiration puis j'ai animé un stand à la kermesse de notre établissement hier.
Et toi ? J'espère que ta semaine a été intéressante ? (Tu peux m'en parler en retour de mail ou via Instagram, je serais très heureux de te lire 😊).
Au programme :
- Je travaille beaucoup mes maths, mais mes notes ne s'améliorent pas...pourquoi ?
- Une idée d'un sujet pour le grand oral pour les terminales #3.
- Le salon Lerning Technologies 2022.
- Mes coups de cœur de la semaine.
🤔 Je travaille beaucoup mes maths, mais mes notes ne s'améliorent pas...pourquoi ?
Cette question revient assez souvent dans mes échanges avec des élèves. Je t'en parle maintenant parce qu'elle m'a de nouveau été posée par une première cette semaine.
Pour répondre à cette question et lever une petite ambiguïté que je remarque souvent, je te prie de considérer la phrase suivant :
La mathématique n'est pas une discipline focalisée sur les savoirs mais sur la manière de les construire.
Cette phrase n'est pas de moi, mais de l'une de mes mentors : Angela Pasquale (Elle a été mon professeur encadrant en 2015...une des meilleurs mathématiciens que je connais et une femme admirable).
Ce qu'elle veut dire par cela est que la connaissance des savoirs mathématiques n'est pas suffisante pour maîtriser l'art de faire des mathématiques. Ce n'est que le début.
Beaucoup d'élèves pensent que faire des exercices en masse est suffisant pour leur garantir de bien réussir les examens. Sauf que cette approche basée sur l'accumulation quantitative ne marche pas au-delà de l'année de seconde. Pourquoi ? Eh bien parce que les mathématiques abordées deviennent tellement riches qu'il y a littéralement une infinité de situations possibles. Cette méthode détourne l'élève de ce qu'il devrait vraiment faire : comprendre en profondeur les notions qu'il manipule afin de pouvoir les utiliser dans une réflexion logique peu importe le contexte.
Je vais te donner une métaphore afin de mieux illustrer mon propos : Un verrier sait façonner du verre pour lui donner toute sorte de formes et d'usages. Il ne te dira jamais : Ah non, je ne fabrique que des bouteilles !
Les savoirs mathématiques sont similaires à du verre à l'état brut : il faut apprendre à les façonner. C'est cette partie qui fait de la discipline un art 😊
Que faire alors ?
Comme un artisan verrier, tu dois apprendre à manipuler tes ressources dans tous les sens. Tes théorèmes et tes définitions ne sont que la matière première de ta pratique.
Le verrier a besoin d'une grande dextérité manuelle pour façonner ses œuvres. De la même façon, tu as besoin de beaucoup de rigueur et de précision pour construire tes démonstrations et écrire des argumentations solides et logiques. Alors au lieu de passer un temps fou à faire des centaines d'exercices sans trop réfléchir...fais en plutôt très peu mais avec une attention très particulière à ce que tu fais, comment tu le fais et aux arguments que tu avances. Soumets-les à l'épreuve de la cohérence logique et regarde si tes propos sont convaincants.
Ce n'est que comme ça qu'on progresse réellement. Car on apprend à réfléchir plutôt qu'à simplement réciter des savoirs.
Et si tu n'y arrives toujours pas (ce que je ne te souhaite pas...tiens ça rime bien !), alors je te conseille de lire le livre suivant :

💡Une idée d'un sujet pour le grand oral pour les terminales #3
Ah, le sujet de cette fois-ci me rend nostalgique. J'ai passé deux ans entières à l'étudier dans tous les sens dans l'espoir d'en percer les secrets...mais en vain ! J'ai nommé la fascinante conjecture de Syracuse (connue aussi sous le nom de la conjecture de Collatz).
Quèsaco ❓
Cette conjecture concerne une suite de nombres entiers positifs très simple à définir. Voici comment elle est construite :
- Choisir un nombre entier positif quelconque.
- Si le nombre est pair, il faut le diviser par 2 sinon il faut le multiplier par 3 puis rajouter 1.
- Itérer le processus avec le résultat obtenu indéfiniment.
En des termes plus mathématiques, voici une définition par récurrence de la suite :
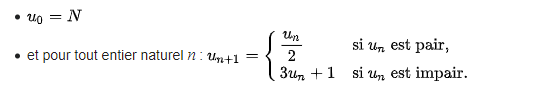
Jusqu'ici, rien de très intéressant diras-tu ? Et si je te disais que quel que soit le nombre N que tu choisiras, la suite se termine toujours avec une boucle fermée des nombres 4-2-1. Ce résultat très surprenant est toujours non démontré à nos jours (à ma connaissance !)
Cette conjecture a tellement fasciné les mathématiciens qu'ils ont trouvé différentes façons de la représenter visuellement. Voici une sélection des plus belles représentations 👇

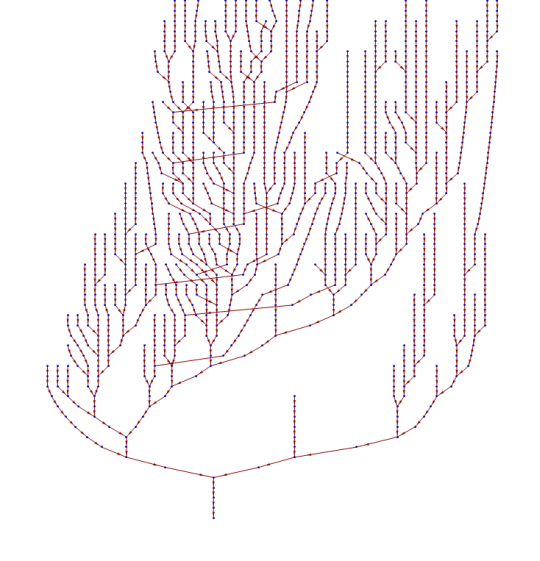
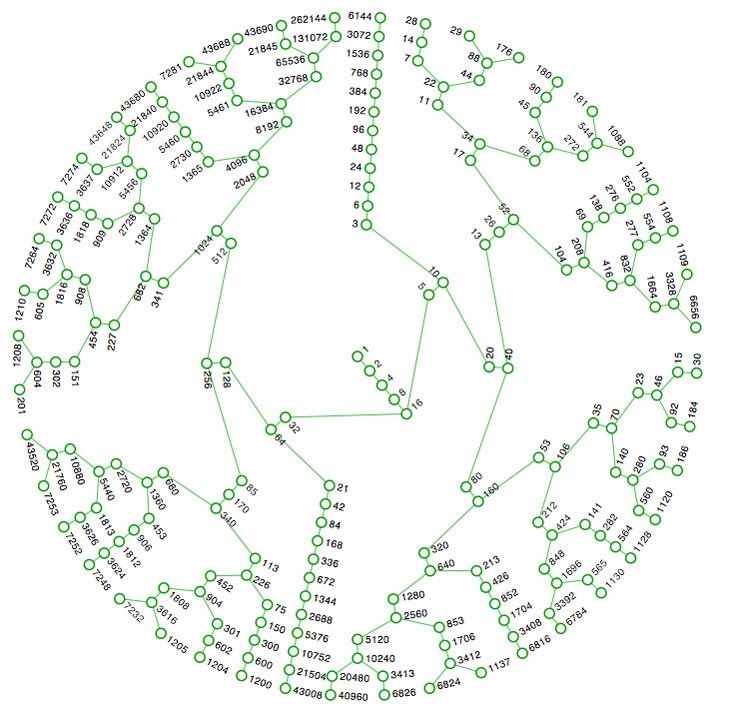
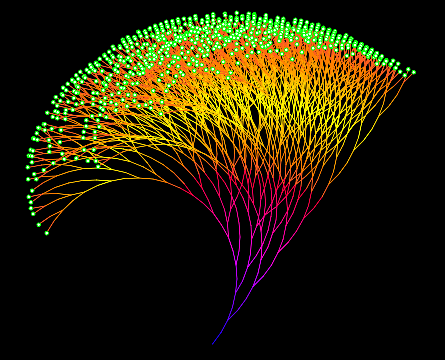

Pour en savoir plus sur cette conjecture, je t'encourage à regarder les vidéos suivantes 👇


La problématique ❓
Ah oui c'est vrai...je me suis laissé emporter dans mon enthousiasme...comme d'habitude 😅
Voici une problématique qui pourrait convenir pour un sujet de grand oral :
Comment les résultats les plus simples à comprendre sont aussi les plus difficiles à démontrer en mathématiques : L'exemple de la conjecture de Collatz.
💇Salon des Learning Technologies
Non, non...pas un salon de coiffure ! Mais plutôt le rendez-vous annuel des professionnels du numérique éducatif en entreprise. Celui-là 👇

Je suis allé le visiter car c'est un lieu inspirant qui regroupe les leaders EdTech et solutions numériques éducatives à destination de la formation continue en entreprise. Certes, ce n'est pas adapté à la formation initiale (collège/lycée) mais on peut toujours y trouver des idées intéressantes et nouvelles.
Mon top pick cette fois-ci était l'entreprise Teach-up : C'est une entreprise qui a développé un outil qui permet de personnaliser l'apprentissage grâce à l'intelligence artificielle.
Pour en savoir plus sur ce salon 👇

💞 Mes coups de cœur de la semaine.
- La Kermesse de mon établissement : Parce que j'y ai passé un moment sympa de partage avec les collègues, parents et élèves. J'ai même pu revoir certains de mes anciens élèves (mention spéciale à Anthony et Valeria !).
- Le retour d'Alexandre sur les pratiques pédagogiques au Canada : La personne concernée va se reconnaître. Nous avons eu un échange très enrichissant (pour moi surtout !) autour de son séjour d'observation dans un lycée au Canada. J'ai notamment été fasciné par leur approche qui utilise la data pour mieux accompagner les élèves et le décloisonnement des classes.
- Veritasium - YouTube : Cette chaîne est une pépite et une source d'inspiration permanente. L'idée de la conjecture de Collatz que je viens de vous présenter (en haut☝️) m'est revenue à l'esprit après avoir vu passer leur vidéo sur le sujet.
Voilà, c'est tout pour cette semaine !
Dis-moi ce que tu en as pensé directement en répondant à ce mail ou bien via Instagram.
Tu as aimé cet e-mail ? Transfère-le à une personne qui te donne le 😊. Elle peut s’inscrire ici.
Tu n'as pas aimé cet e-mail ? Transfère-le à une personne que tu n'aimes pas. Elle peut s’inscrire ici. 😁












Discussion entre membres