#3🙄 Le bac de maths 2022...bof !

Salut cher(e) ami(e) 👋

L'examen de spécialité en mathématiques a eu lieu de cette semaine. Comme la plupart des professeurs, j'ai dû surveiller le déroulement des épreuves. Et puisque c'est la première épreuve de Bac de mathématiques postréforme, j'étais très curieux de voir les sujets proposés.

C'était une déception complète 🙄

Au programme :

1. Les examens de spécialité...qui ne spécialise en rien !
2. Une idée d'un sujet pour le grand oral pour les terminales #2.
3. Écrire pour mieux réfléchir : Les systèmes de prise de notes.
4. Mes coups de cœur de la semaine.

📃 Les examens de spécialité...qui ne spécialise en rien !

Quand j'ai entendu parler de la réforme pour la première fois, j'étais sincèrement très enthousiaste. L'idée était, du moins en théorie, très prometteuse.

Donner aux élèves la possibilité de choisir leurs matières puis d'en faire de vrais spécialistes en approfondissant davantage les notions et en augmentant le seuil des exigences (qui était jusqu'alors au ras des pâquerettes !) est une idée qui a tout pour séduire le mathématicien que je suis.

Bien évidemment, la promesse était trop belle pour être vraie 😑

Je vais taire ici les aspects organisationnels internes à l'E.N qui rendent ce rêve très irréalisable (à l'échelle nationale bien évidemment, car c'est tout à fait atteignable localement) et je vais me concentrer sur la dernière preuve de sa faillite intellectuelle : Ce qu'est devenu l'examen du Bac.

Afin que tu puisses t'en rendre compte, je vais procéder à l'inventaire des "aménagements" du bac de mathématiques 2022 :

1. L'examen ne porte pas sur l'option mathématique experte pour ceux qui l'ont choisi alors que c'était le cas pour l'option équivalente dans l'ancien bac.
2. Beaucoup...beaucoup moins de contenu au programme de l'examen. Les intégrales ne sont plus évaluables en examen national par exemple.
3. 4 sujets sont proposés aux élèves dont un QCM. (C'est déjà un GROS aménagement d'avoir un QCM)
4. Ils doivent en traiter seulement 3 (la cerise sur le gâteau) en 4 heures.

Alors, je vais te poser une petite question : Est-ce que ma liste ci-dessus est cohérente avec l'idée principale de former des "spécialistes" ?

Fin de l'argumentaire !

Si tu souhaites jeter un coup d'œil aux épreuves et aux corrections 👇

Baccalauréat spécialité maths 2022 6 sujets 5 corrigés

Polynésie 4 mai 2022 sujet 1 Corrigé Polynésie 4 mai 2022 sujet 1 Polynésie 5 mai 2022 sujet 2 Corrigé 1 Polynésie 5 mai 2022 sujet 2 Corrigé 2 Polynésie 5 mai 2022 sujet 2 Métropole Antilles-Guyane 11 mai 2022 sujet 1 Corrigé Métropole Antilles-Guyane 11 mai 2022 sujet 1 Centres étrangers 11 mai 20…

APMEPAPMEP

💡Une idée d'un sujet pour le grand oral pour les terminales #2

La semaine dernière, je t'ai donné une idée de mathématiques appliquées au sport (Si tu as raté cela, tu peux aller lire : ICI). Cette semaine, je reviens à un sujet bien plus théorique : Le triangle de Tribonacci (et non, ce n'est pas une erreur de frappe 😅).

Si tu es l'un de mes élèves, alors tu sais bien à quel point j'adore la suite de Fibonnaci et le triangle de Pascal qu'elle engendre. D'ailleurs, si tu es en terminale, alors tu as déjà eu le plaisir de traiter ces notions-là.

Petit rappel : la suite de Fibonnaci est la suite qui commence par les deux nombres : 0 et 1 et qui construit l'élément suivant en tant que somme des deux précédents. On obtient alors une séquence infinie du type : 0 ; 1 ; 1 ; 2 ; 3 ; 5 ; 8 ; ...

Cette séquence apparaît de manière très inattendue dans le triangle de Pacal lorsqu'on fait la somme des diagonales. 👇

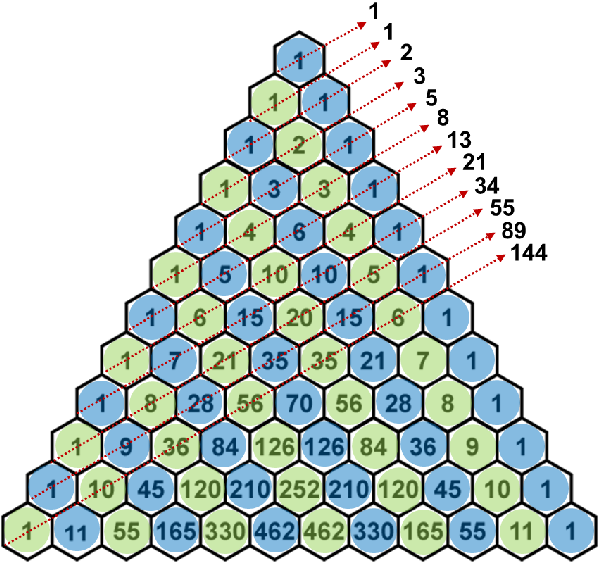
Passons, Fibonnaci n'est pas le sujet ici (même si je peux en parler pendant des heures 😂). C'est Tribonacci qui nous intéresse !

Quèsaco ❓

Eh bien, c'est presque la même idée que la suite de Fibonnaci...sauf qu'on additionne trois nombres consécutifs pour trouver le suivant :

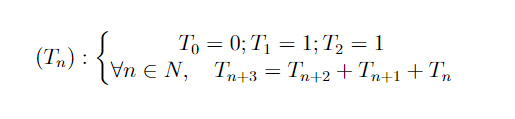
Cela donne également naissance un petit frère très élégant au triangle de Pascal que voici :

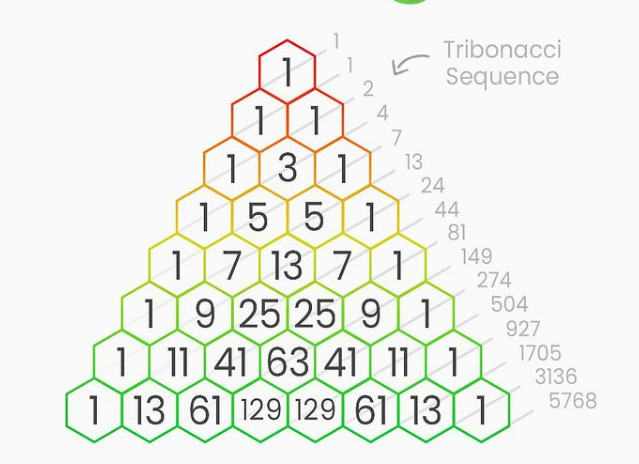
J'imagine que tu as compris quelle est la problématique du jour, n'est pas ? Si ce n'est toujours pas le cas, voici une proposition de formulation :

Comment construire le triangle de Tribonacci en analogie avec le triangle de Pascal ?

Si tu souhaites en savoir plus sur le sujet et que tu es doué en anglais, alors je te propose de lire l'article suivant :

Ou alors tu peux aussi m'écrire pour en parler : rguejdad@acmathematica.com

⚠️ Un avertissement quand même, âmes sensibles s'abstenir 😅

🖋️ Écrire pour mieux réfléchir : Les systèmes de prise de notes.

Je vais commencer cette section par citer Jordan B. Peterson :

The primary reason to write is so that the writer can formulate and organize an informed, coherent and sophisticated set of ideas about something important

Oui, je sais...pas besoin de me faire remarquer à quel point je suis influencé par des courants anglophones. 😅

Mais revenons au cœur du sujet. Je vais partir d'une croyance personnelle : Il faut écrire pour construire une réflexion logique et bien argumentée. C'est très vrai en mathématiques, mais je pense que cela s'applique à tout effort intellectuel.

Sauf qu'écrire sur un papier (ou tout autre support s'y assimilant) me pose un petit souci personnel : La dimension linéaire de la pensée. Je m'explique : Quand tu écris sur un papier ou sur un Word par exemple, tu es toujours prisonnier d'un format qui t'impose d'aller dans un seul sens (de haut en bas). Dans une écriture très linéaire.

Mais heureusement, avec les nouvelles technologies, il est maintenant possible de sortir de ce format en exploitant l'horizontalité. Des outils comme notion ou encore Obsidian le permettent assez facilement en liant des documents parallèles.

J'ai déjà parlé de notion ici 👇

⏳Et si vous perdiez moins de temps à travailler vos cours ?

Que vous soyez un élève ou un professeur, optimiser votre journée et tirer le maximum de votre temps de travail n’est pas un luxe, c’est une nécessité !

Rachid GuejdadRachid Guejdad

Et si tu souhaites en savoir plus sur Obsidian, je te conseille d'aller voir par là.👇

Obsidian

Obsidian: A knowledge base that works on local Markdown files.

Tu l'auras compris, ces deux outils sont mes recommandations EdTech de la semaine. Souhaites-tu en savoir plus sur les potentiels usages de ces outils pour un élève ou un professeur ? Si oui, alors n'hésite pas à m'en toucher deux mots en répondant à ce mail !

💞 Mes coups de cœur de la semaine.

1. Un échange intéressant avec une inconnue sur LinkedIn : J'ai partagé un post LinkedIn sur l'épreuve du bac et à quel point je suis admiratif des élèves de cette année (vu toutes les circonstances...y compris celles mentionnées au début de ce mail). Une dame que je ne connais pas du tout a commenté mon post et nous avons eu un bref échange assez sympathique. Tu peux le retrouver : Ici
2. Un échange avec un de mes anciens élèves : Tu l'auras remarqué, j'adore échanger (n'hésite donc pas à me contacter pour discuter via e-mail, sur Instagram ou LinkedIn).
   Mayeul (que je salue fortement s'il me lit ici!), un de mes anciens élèves m'a envoyé son programme de mathématiques à l'EPFL après une petite discussion. Comparer les programmes universitaires suisses à ce qui se fait en France est très intéressant jusqu’ici !
3. Synapses - YouTube : Ma découverte économique de la semaine ! Une chaîne qui aborde les défis économiques actuels via des interviews avec des experts qui sont très pédagogues. Si tu es un élève qui souhaite faire des études d'économie ou une école de commerce par la suite, je te conseille vivement d'y jeter un coup d'œil.

Voilà, c'est tout pour cette semaine !

Dis-moi ce que tu en as pensé directement en répondant à ce mail ou bien via Instagram.

Tu as aimé cet e-mail ? Transfère-le à une personne qui te donne le 😊. Elle peut s’inscrire ici.

Tu n'as pas aimé cet e-mail ? Transfère-le à une personne que tu n'aimes pas. Elle peut s’inscrire ici. 😁