#16❎Ne plus avoir peur de l'échec en mathématiques.

Salut cher(e) ami(e) 👋,

Les vacances de la Toussaint arrivent à grand pas...j'ai hâte ! J'imagine que toi également ?

Mais avant cela, il nous reste quand même une petite semaine de travail intensif, d'évaluations et de DST...de corrections, si tu es professeur. Ce contexte génère souvent du stress et un peu de pression. Mais il ne faut pas y succomber !

Comme souvent, c'est une discussion avec des élèves qui me poussent à parler du sujet de la journée : Le rapport à l'échec. Dans notre tradition bien française, je trouve qu'il est souvent à l'origine de bien des problèmes dans les salles de classe.

❎ La peur de l'échec en mathématiques. Comment éviter d'être paralysé face au challenge de la difficulté.

Il m'arrive souvent, en observant des élèves, d'en voir certains qui sont paralysés dans l'inaction. Ils n'essayent même plus lorsqu'on leur demande de résoudre un exercice mathématique. Ils sont résignés. Quand je les encourage à se lancer, les réponses que j'ai en retour sans souvent des tentatives maladroites et gênées qui cherchent à me faire comprendre le message suivant :

De toute façon, je sais que je vais me tromper, donc je n'essaye même plus.

Bien évidemment (et fort heureusement), aucun élève ne m'a jamais répondu comme cela. Mais il n'est pas difficile de déchiffrer le message derrière les réponses diplomatiques des élèves. Et c'est encore moins le cas, lorsqu'un élève ne répond pas à une question lors d'une évaluation, ou pire...rend copie blanche.

Certains diront que ces élèves manquent de motivation ou encore qu'ils sont faignants. Je pense pour ma part qu'ils ont surtout peur de se tromper !

Je pense que notre système scolaire ne laisse pas assez d'occasions aux élèves pour qu'ils fassent des erreurs. Ces derniers ont associé les mots 'erreur' et 'mal'. Pourtant c'est exactement ce qu'il ne faut pas faire dans sa quête d'excellence en mathématiques. Car c'est avant tout, en faisant des erreurs, qu'on progresse !

Les raisons pour cela sont diverses, je vais en citer quelques-unes :

1. La perfection ne fait pas partie du champ des possibles des humains. Tout ce que nous produisons est perfectible. Pourquoi s'en vouloir alors d'échouer à une tâche ?
   Si l'on considère que réussir une action est de l'exécuter à la perfection, alors tout le monde est en train d'échouer en permanence non ?
   Heureusement, cette vision utopiquement absolue de la réussite n'est pas celle que l'on se définit !
   Pour ma part, je considère que j'ai réussi quelque chose (ou que je suis en train de le réussir) à partir du moment où ma dernière tentative est meilleure que la précédente. C’est-à-dire quand je constate un progrès. Certes, ce n'est pas parfait...mais c'est toujours mieux que ce que je faisais (avais) avant ! Et toi ? Quelle est ta définition de la réussite ?
2. Ce sont les échecs qui nous aident le plus à progresser et non les réussites. Ai-je besoin de te parler de l'histoire d'Edison et de son ampoule électrique ? Pas besoin, je suis sûr que tu la connais déjà !
   La morale est que, c'est en analysant ses erreurs qu'on progresse. Sauf que, pour avoir des choses à analyser...il faut déjà commencer par se tromper ! 😅
3. L'essai/erreur est ton meilleur ami ! Bon, peut-être pas le jour d'une évaluation. Mais c'est en se donnant le droit d'essayer pour se tromper dans des conditions favorables (lors de séances d'exercices, lorsque tu révises à la maison...etc.) qu'on évite de le faire lors des échéances décisives.
4. Les mathématiciens se trompent tout le temps. Je dis souvent à mes élèves que les mathématiciens passent leur temps à se tromper. Souvent, ils ont du mal à me croire. Et pourtant c'est vrai !
   J'avoue que la façon dont nous enseignons les mathématiques y est pour quelque chose : Lorsqu'un professeur expose un résultat mathématique dans un cours, il le fait d'une façon linéaire, optimale et directe (car les heures de cours sont limitées). Les élèves ont donc la fausse impression que cela lui vient facilement et sans recherche. Ces derniers oublient que ce qui est exposé au tableau n'est pas l'œuvre de leur professeur, mais l'effort cumulé de beaucoup de mathématiciens à travers les âges. Qu'il a fallu que beaucoup de personnes se trompent pendant longtemps afin d'arriver aux beaux résultats qu'on expose en classe. 😉

Il y a encore beaucoup de choses à dire à ce sujet, mais je vais devoir m'arrêter là. Les copies de DST de mes premières attendent. 😅

Mais en tout cas, accorde-toi le droit de te tromper. Si même le service des impôts te l'accorde, alors pourquoi t'en prives-tu de ton propre chef ?

Et si tu penses que les mathématiques sont compliquées, je te laisse cette citation de Von Neumann.

Si les gens ne croient pas que les mathématiques sont simples, c’est uniquement parce qu’ils ne réalisent pas à quel point la vie est compliquée.

🔢 16...comme le seul carré d'entiers interchangeable.

On dit souvent qu'une image est plus parlante que mille mots. Donc, avant de te parler en détail du nombre 16, admire ce chef-d’œuvre 👇

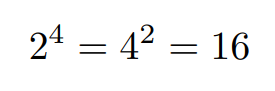
À première vue, cette égalité n'a rien d'intéressant n'est-ce pas ? Pourtant, elle n'est pas du tout banale. La raison ? Les nombres 2 et 4 sont les uniques entiers naturels qui peuvent être interchangés entre base et exposant pour obtenir exactement le même nombre : 16.

Tut, tut, tut ! Je t'ai vu venir. Tu vas contre argumenter, en disant que cela marche si j'expose n'importe quel entier à lui-même (3 puissance 3 par exemple). C'est vrai...mais 2 et 4 forment le seul couple de nombres distincts vérifiant cette propriété. 😁

🤯 Le dernier théorème de Fermat...le théorème qui résista 300 ans !

Puisque je t'ai parlé de l'échec en mathématiques, je vais te donner l'un des exemples qui illustrent le plus ses bienfaits.

L'image ci-dessous représente une page de la réédition, qui date de 1670, du livre de Diophante d'Alexandrie (mathématicien grec du 3ème siècle) .

Ce qui nous intéresse ici, n'est pas le livre de Diophate en lui-même, mais ce que cette édition à de particulier : Elle contient les annotations de Pierre de Fermat.

Il énonce sur cette page (le cadre rouge), l'un des plus célèbres théorèmes en mathématiques : Le dernier théorème de Fermat.

Ce théorème, bien qu'il ait été énoncé au 17ème siècle, ne sera démontré totalement qu'en 1995. Je n'ai pas besoin de te préciser que bien des mathématiciens se sont essayés à le démontrer en plus de 350 ans...et qu'ils ont donc tous, essuyé de cuisants échecs (des échecs partiels a minima).

Andrew Wiles est le mathématicien qui vient au bout de ce calvaire ! Il travailla d’arche pied, et dans le secret total pendant 8 ans pour trouver une solution. Il présentera ses premiers résultats lors d'une conférence d'été en 1993. Mais à son grand malheur, une faille énorme sera repérée dans sa démonstration...

Monsieur Wiles était désespéré ! Comment allait-il s'en sortir maintenant alors qu'il est sous le feu des projecteurs ? Il risquait littéralement sa réputation de mathématicien et il devrait absolument trouver une solution. Mais il n'y arrive pas, il est à bout de forces et se résigne à l'échec.

Pourtant ! Richard Taylor (un autre mathématicien) lui suggérera une idée qui finira par tout dénouer neuf mois plus tard...L'honneur était sauf et l'un des plus épineux théorèmes de l'histoire des mathématiques a été démontré !

Wiles parle avec beaucoup de nostalgie de cette partie de sa vie, il est content de l'avoir vécu et il est surtout content d'avoir su se hisser au-delà de son échec initial.

J'adore cette histoire car elle montre à quel point surmonter les échecs et les difficultés est au cœur de la discipline. Si même des mathématiciens brillantissimes comme Wiles doivent affronter et surmonter leurs échecs alors il est également de notre devoir de faire de même. Je finirai par citer l'un de mes anciens professeurs :

Il faut savoir être humble face aux mathématiques. Si même les plus grands doivent d'abord se tromper, alors qui sommes-nous pour s'attendre à réussir du premier coup ?

🎦 Youtube Math find :Hervé Lehning nous parle des problèmes du millénaire.

Tu l'auras compris, le numéro d'aujourd'hui met à l'honneur les problèmes mathématiques qui ont donné, et qui donnent encore, du fil à retordre aux mathématiciens. Voici une petite vidéo à propos des problèmes du millénaire. Ces questions mathématiques dont la résolution vous vaudra une récompense d'un million de dollars. Bonne chance ! 😅

💞 Mes coups de cœur de la semaine

Cette fois-ci, je n'en ai qu'un à mentionner. Mais il me suffit largement !

Une lectrice m'a écrit cette semaine pour me dire que la lettre du dimanche l'aide à préparer un concours (elle se reconnaîtra j'en suis sûr !).

Alors un grand merci pour le très gentil message. Cela me fait toujours plaisir de lire les retours et d'échanger avec vous tous.

Si tu as un petit moment, n'hésite pas à m'écrire. Je lis et réponds à tous les courriels que je reçois.