Salut cher(e) ami(e) 👋,

Tu as probablement fait ta rentrée scolaire en fin de la semaine dernière. Nous y sommes enfin !

La mienne est synonyme de changement cette année. Si tu es un nouveau lecteur, tu ne le sais probablement pas, mais j'ai décidé de changer d'établissement scolaire cette année. Je suis donc très heureux de faire ma première rentrée au Lycée Notre Dame de Boulogne. 😀

Et toi ? Comment s'est passée ta rentrée ? Es-tu satisfait de ta classe, tes professeurs... ? N'hésite pas à m'écrire un petit mail pour m'en parler. 😉

Je te souhaite une belle rentrée...pleine de mathématiques 😁

🔍Comment travailler efficacement ses mathématiques et ne pas prendre de retard ?

Cette question revient très souvent dans mes discussions avec des élèves. Plusieurs d'entre eux me disent qu'ils travaillent de manière régulière et qu'ils font beaucoup d'exercices mais en vain !

Ils ont souvent l'impression que le lycée est plus dur que le collège car la méthodologie qu'ils ont utilisée, et qui a très bien marché dans le premier, ne donne plus aucun résultat satisfaisant. Où alors peu de résultats vu l'effort engagé. Ils finissent par perdre pied et de lâcher l'affaire suite aux déceptions successives.

Si tu te reconnais dans cette situation, eh bien sache que ce n'est pas parce que tu es nul ou moins intelligent que les autres. Tu dois juste adapter ta méthodologie de travail.

Un de mes anciens professeurs du lycée a résumé ce que je vais t'expliquer par la suite en une seule phrase :

Là où le collège favorise les approches quantitatives et mécaniques, le lycée les sanctionne.

Pendant tes années au collège, tu avais probablement l'habitude de faire beaucoup d'exercices de mathématiques. Le schéma de révision de la plupart des élèves est le suivant :

  1. J'apprends par cœur mes formules.
  2. Je retravaille les exercices faits en classe.
  3. Je fais beaucoup d'exercices similaires.

Cette méthode est principalement basée sur ta capacité à retenir et à mémoriser. Tu cherches à faire des exercices qui couvrent toutes les situations possibles dans l'espoir d'avoir une situation similaire lors de ton évaluation.

Ce n'est pas une mauvaise façon de faire les choses...c'est suffisant au collège, mais c'est loin d'être efficace.

Le problème au lycée, c'est que le nombre de situations possibles est quasiment infini. Cela est du principalement à la complexité des notions abordées. Cette approche devient donc complètement obsolète. Mais comment faire alors ? 🤔

La réponse est la suivante 👇

Tu dois faire une transition d'une méthode basée sur la mémorisation vers une autre qui est basée sur la réflexion et la compréhension.

Tu dois passer beaucoup plus de temps sur ton cours afin de comprendre pourquoi et comment sont amenés les résultats que tu utilises. Tu ne cherches plus à faire un maximum d'exercices, mais plutôt à faire des exercices de grande qualité. Le but ? Maîtriser les outils plutôt que les situations. Je vais illustrer mes propos pour plus de clarté : Imagine que tu es un mécanicien qui répare des voitures. Au début, tu sais qu'un tournevis te permet de tourner des vis (jusqu'ici rien de miraculeux 😅). Un mécanicien débutant va donc se contenter de l'utiliser à chaque fois qu'il voit un vis...rien de plus ! Un mécanicien expérimenté quant à lui, comprends et maîtrise beaucoup plus son outil...Il lui trouve donc plein d'utilisations supplémentaires : ouvrir une boîte de peinture...

Ton tournevis à toi, ce sont les notions mathématiques. Tu dois les comprendre à un degré tel que tu peux voir comment les utiliser dans toutes les situations que tu vas croiser.

Pour faire cela, rien de mieux qu'une méthode active de révision. J'en parle en détail dans ce post Instagram 👇

➕ Le théorème de Nicomaque...un drôle de résultat !

Nicomaque de Gérase est un mathématicien qui a vécu au premier siècle après J.C en ce qui sera connue comme la Jordanie. Il appartient au courant néo-pythagoricien. Le résultat que je vais te présenter aujourd'hui lui est souvent attribué même s'il n'est pas vraiment le seul à l'avoir découvert. Il s'agit de l'égalité suivante :

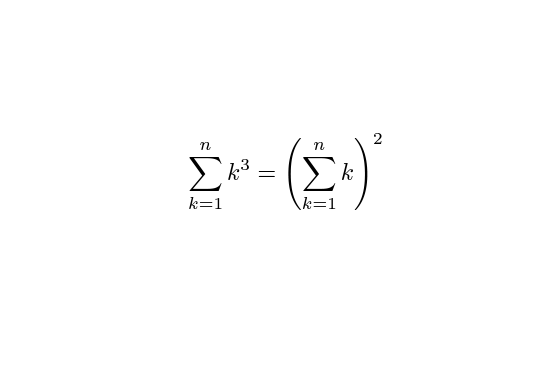
La somme des cubes des n premiers entiers est égale au carré de la somme de ces derniers.

Le jour où j'ai découvert ce résultat pour la première fois, je suis resté bouche bée ! Cette égalité est tellement improbable que je n'en reste pas moins émerveillé aujourd'hui. 🤯

Je vais expliquer avec un peu plus de détails : cette égalité te dit que si tu prends une série d'entiers consécutifs en partant de 1 (1;2;3;4 par exemple) alors tu peux écrire ceci :

Un raccourci de malade !!

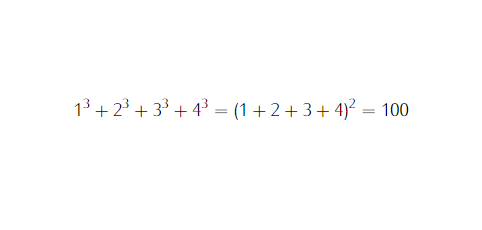
Impressionnant ! N’est ce pas ?

Ce que je trouve encore plus magique, c'est la visualisation de cette identité comme image. Voici une illustration qui décrit ce résultat 👇

Illustration qui démontre le résultat jusqu'au rang 5.

Ce résultat plutôt facile à démonter si tu sais utiliser une récurrence (niveau terminale), mais il y a également d'autres démonstrations plus accessibles pour les niveaux inférieurs. Je te laisse t'amuser avec 😉

📖 Lecture de la semaine : A mind for numbers.

Dans la continuité de ma discussion autour des méthodologies de travail des mathématiques au lycée, je te propose aujourd'hui un livre que je recommande à tous les élèves qui ont du mal à travailler les mathématiques. Il s'agit d'un livre nommé : A mind for numbers et écrit par Barbara Oakley.

A mind for numbers.

Barbara Oakley

Je n'ai pas encore fait de résumé à son sujet, mais je ne vais probablement pas tarder à le faire. Professeur Oakley est une mathématicienne et spécialiste de l'apprentissage. Elle t'explique dans ce livre comment t'y prendre pour adopter une méthode de travail qui va t'aider à réussir en sciences et plus spécifiquement en mathématiques. Je crois qu'il a été traduit en français, mais je n'en suis pas certain.

🎦Youtube Math find : Le plus simple problème de mathématiques que personne n'arrive à résoudre.

Il y a beaucoup de résultats mathématiques qui me fascinent ! Je viens de te parler de l'égalité de Nicomaque. Un autre résultat que je trouve fascinant est la conjecture de Collatz (ou de Syracuse). J'en ai déjà parlé dans une lettre précédente, mais vu que j'ai, de nouveau, revu la vidéo de Véritasium à ce sujet, je te la partage. 👇

Vidéo de Veritasium.

💞 Mes coups de cœur de la semaine

Il y en a plusieurs cette fois-ci 😁

  1. Un échange en Visio avec Edouard : Bon, tu le sais maintenant, j'adore parler avec mes anciens élèves. J'ai donc été très heureux de passer une heure à discuter avec Edouard, un de mes anciens élèves qui fait une prépa commerce maintenant. Nous avons eu un échange très sympa autour de l'entrepreneuriat et la quête de sens dans le travail.
  2. Vos retours sur Instagram : Je vous ai demandé hier dans une story Instagram de me donner des nouvelles de votre rentrée. Vous êtes plusieurs à l'avoir fait et c'était vraiment chouette. 😀
    Je vous souhaite à tous une belle rentrée !
  3. L'organisation de mon nouvel établissement et l'accueil que j'ai eu : J'ai été très bien reçu et accueilli en compagnie de tous les nouveaux professeurs dans mon nouvel établissement. Cela paraît normal, mais je peux vous assurer que ce n'est pas toujours le cas ! Alors un grand merci aux équipes de LNDB.